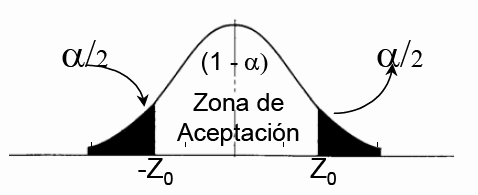
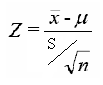Distribuciones de muestreo
Si las variables aleatorias x1.x2...........xn. tienen la misma función de densidad de probabilidad que la de la distribución de la población, entonces x1.x2............xn forman un conjunto de n variables aleatorias independientes e idénticamente distribuidas (IID) que constituyen una muestra aleatoria de la población.
Teorema de Limite Central
Sean x1.x2.........xn, n variables aleatorias independientes idénticamente distribuidas con media m y varianza s2 ambas finitas. La suma de esas variables Sn = x1+x2+ ...+ xn es una variable aleatoria con media nm y varianza ns2, entonces
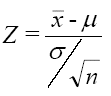
se distribuye como una normal N(0;1). En otras palabras, el teorema expresa que cuando n crece sin límite, la variable z tiende a distribuirse normalmente. Si las variables no son idénticamente distribuidas, se podría demostrar igualmente que: z =  se distribuye como una normal N(0;1), es decir que la suma de variables independientes tiende a ser normal con media suma de medias y varianza suma de varianzas.
se distribuye como una normal N(0;1), es decir que la suma de variables independientes tiende a ser normal con media suma de medias y varianza suma de varianzas.
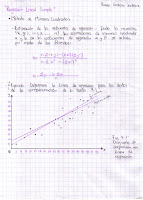
La aproximacion a la 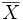
depende del tamaño de la muestra.
Se concluye que la media de la medias va a ser igual a la media de la poblacion.
Cual es el tamaño adecuado de la distribucion?Si el tamaño de la muestra es menor que 30 se puede aplicar el teorema de limite cental para una poblacion con cualquier tipo de distribucion de probabilidad.
Si el tamaño de la muestra es menor que 30 es necesario asegurarse que la distribucion de probabilidad de la poblacion es normal.
Diferencia de Medias
Sean dos poblaciones con media μ1 y μ2 y var1 y var2:

*El tamaño de la muestra debe ser mayor o igual a 30.
Distribucion "t"Se usa en el caso en que tenemos una poblacion normal pero el tamaño de la muestra es pequeño y varianza poblacional desconocida.



- Intervalo de confianza: nivel de seguridad de que el valor observado caiga dentro del parametro.
Problema distribucion "t"
El fabricante de un propulsor utilizado en un sistema de escape de emergencia le gistaria afirmar que su producto tiene una tasa promedio de 40in/min para investigar esta informacion el fabricante pureba 25 granos de propulsor, seleccionados al azar, y si el valor de t calculado cae entre -to.o5, 24 y to.o5, 24 entonces queda satisfecho. A que conclusion debe llegar el fabricante si tiene una muestra con una media de 42,5 in/min y una desviacion estandar muestral de 0.75 in/min.
Supongase que la tasa del propulsor tiene una distribucion normal.
n= 25
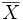 =42.5
=42.5
S=0.75
μ= 40

=(42.5 - 40)/(o.75/5)
= 2.5/(0.15)
t = 16.66
Distribución χ²
En estadistica, la distribución ji-cuadrada, también denominada ji-cuadrado de Pearson, es una distribucion de probabilidad
continua con un parámetro
k que representa los grados de libertad de la variable aleatoria:

donde Zi son variables de distribucion normal, de media cero y varianza uno.
Distribucion "F"
Supóngase que deseamos comparar las varianzas de dos poblaciones normales basados en la información contenida en muestras aleatorias independientes de las poblaciones. Supóngase que una muestra aleatoria contiene n1 variables aleatorias distribuidas normalmente con una varianza común  y que la otra muestra aleatoria contiene n2 variables aleatorias distribuidas normalmente con una varianza común
y que la otra muestra aleatoria contiene n2 variables aleatorias distribuidas normalmente con una varianza común  . Si calculamos
. Si calculamos  de las observaciones en la muestra 1, entonces
de las observaciones en la muestra 1, entonces  es una estimación de
es una estimación de  . De manera similar
. De manera similar  calculada a partir de las observaciones de la segunda muestra es una estimación para
calculada a partir de las observaciones de la segunda muestra es una estimación para  . Así intuitivamente podríamos pensar en utilizar
. Así intuitivamente podríamos pensar en utilizar  para hacer inferencias con respecto a las magnitudes relativas de
para hacer inferencias con respecto a las magnitudes relativas de  y
y  ; si dividimos cada
; si dividimos cada  por
por  entonces la razón siguiente:
entonces la razón siguiente:
 =
=  tiene
tiene Prueba de Hipotesis
El nivel de confianza determina los valores criticos.
-Se pruebab los parametros de la poblacion y esos parametros se han obtenido por experiencia en el proceso.
Tipos de Hipotesis
- Bilaterales
- Unilaterales

Ho: Hipotesis Nula: Hipotesis que se pone a prueba.
H1: Hipotesis Alternativa: Hipotesis que se intenta probar.
Hipotesis Bilateral
Ho:
μ=50
H1: μ=! 50
Hipotesis Unilateral
Ho:
μ<50>μ>50
- Pasos para resolver un problema en el que usamos hipotesis.
1. Del contexro del problema, identificar el parametro de interes.
2. Establecer la hipotesis nula.
3. Especificar una apropiada hipotesis alternativa.
4. Seleccionar el nivel de significancia  (alfa)
(alfa)
5. Establecer un estadistico apropiado.
6. Establecer la region de rechazo.
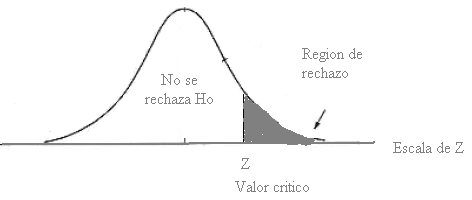
7. Calcular las cantidades muestrales y sustituir en el estadistico.
8. Decidir si se debe rechazar la hipotesis.
Si Z> z o Z< -z 9. Conclusion.
*Un Parametro es una caracterización numérica de la distribución de la población de manera que describe, parcial o completamente la función de densidad de población de la característica de interés.
*Una Estadística (un estadístico) es cualquier función de las variables aleatorias que se observaron en la muestra, de manera que esta función no contiene cantidades desconocidas.
*La distribución de muestreo de una estadística es la distribución de probabilidad que puede obtenerse como resultado de un número infinito de muestras aleatorias independientes, cada una de tamaño n provenientes de la población de interés.
En la siguiente tabla se muestran las decisiones que pueden tomar el investigador y las consecuencias posibles.
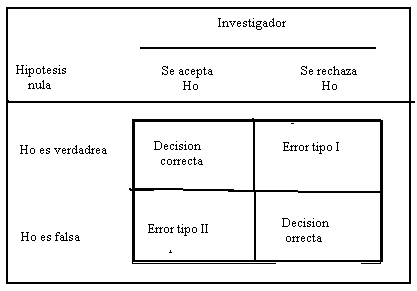
Ejemplo: Los sistemas de escae de emergencia para tripulaciones de aeronaez son impulsados por un combustible solido, una de las caracteristicas importantes de este producto es la rapidez de combustion, las especificaciones requieren que la rapidez promedio de combustion sea de 50 cm/s. Se sabe que la desviacion estandar de la poblacion es 2 cm/s. El experimento decide especificar una probailidad para el error tipo 1, con nivel de significancia de 0.05. Selecciona una muestra aleatoria de 25 y obtiene una rapidez promedio muestral de combustion de 51.3 A que conclusion debemos llegar? D.E.= 2 cm/s nivel de sig.= 0.05 n= 25 Ho:
μ=50 H1: μ=! 50Z= (51.3 - 50)/(2/5)
= 1.3/0.4
= 0.325
Region de Rechazo
zo.o5= 1.96
- zo.o5=-1.96
Z> z o Z< -z
por lo tanto, la produccion no esta cumpliendo con las especificaciones de que el promedio de combustion sea de 50 cm/s.
Ejemplo
El jefe de la Biblioteca Especializada de la Facultad de Ingeniería Eléctrica y Electrónica de la UNAC manifiesta que el número promedio de lectores por día es de 350. Para confirmar o no este supuesto se controla la cantidad de lectores que utilizaron la biblioteca durante 30 días. Se considera el nivel de significancia de 0.05
Datos:
| Día | Usuarios | Día | Usuarios | Día | Usuario |
| 1 | 356 | 11 | 305 | 21 | 429 |
| 2 | 427 | 12 | 413 | 22 | 376 |
| 3 | 387 | 13 | 391 | 23 | 328 |
| 4 | 510 | 14 | 380 | 24 | 411 |
| 5 | 288 | 15 | 382 | 25 | 397 |
| 6 | 290 | 16 | 389 | 26 | 365 |
| 7 | 320 | 17 | 405 | 27 | 405 |
| 8 | 350 | 18 | 293 | 28 | 369 |
| 9 | 403 | 19 | 276 | 29 | 429 |
| 10 | 329 | 20 | 417 | 30 | 364 |
Solución: Se trata de un problema con una media poblacional: muestra grande y desviación estándar poblacional desconocida.
Seleccionamos la hipótesis nula y la hipótesis alternativa
Ho: μ═350
Ha: μ≠ 350
Nivel de confianza o significancia 95%
α═0.05
Calculamos o determinamos el valor estadístico de prueba
De los datos determinamos: que el estadístico de prueba es t, debido a que el numero de muestras es igual a 30, conocemos la media de la población, pero la desviación estándar de la población es desconocida, en este caso determinamos la desviación estándar de la muestra y la utilizamos en la formula reemplazando a la desviación estándar de la población.
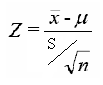
Calculamos la desviación estándar muestral y la media de la muestra empleando Excel, lo cual se muestra en el cuadro que sigue.
| Columna1 |
| Media | 372.8 |
| Error típico | 9.56951578 |
| Mediana | 381 |
| Moda | 405 |
| Desviación estándar | 52.4143965 |
| Varianza de la muestra | 2747.26897 |
| Curtosis | 0.36687081 |
| Coeficiente de asimetría | 0.04706877 |
| Rango | 234 |
| Mínimo | 276 |
| Máximo | 510 |
| Suma | 11184 |
| Cuenta | 30 |
| Nivel de confianza (95.0%) | 19.571868 |
Formulación de la regla de decisión.
La regla de decisión la formulamos teniendo en cuenta que esta es una prueba de dos colas, la mitad de 0.05, es decir 0.025, esta en cada cola. el área en la que no se rechaza Ho esta entre las dos colas, es por consiguiente 0.95. El valor critico para 0.05 da un valor de Zc = 1.96.
Por consiguiente la regla de decisión: es rechazar la hipótesis nula y aceptar la hipótesis alternativa, si el valor Z calculado no queda en la región comprendida entre -1.96 y +1.96. En caso contrario no se rechaza la hipótesis nula si Z queda entre -1.96 y +1.96.
Toma de decisión.
En este ultimo paso comparamos el estadístico de prueba calculado mediante el software Minitab que es igual a Z = 2.38 y lo comparamos con el valor critico de Zc = 1.96. Como el estadístico de prueba calculado cae a la derecha del valor critico de Z, se rechaza Ho. Por tanto no se confirma el supuesto del Jefe de la Biblioteca.
Conclusiones:
- Se rechaza la hipótesis nula (Ho), se acepta la hipótesis alterna (H1) a un nivel de significancia de α = 0.05. La prueba resultó ser significativa.
- La evidencia estadística no permite aceptar la aceptar la hipótesis nula.


![]()

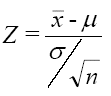

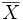 depende del tamaño de la muestra.
depende del tamaño de la muestra.