probabilidad y estadistica: Datos no agrupados/Medidas de dispersion

Rango

El rango estadístico es la diferencia entre el valor mínimo y el valor máximo en un grupo de números. Para averiguar el rango de un grupo de números:

Ordenamos los números según su tamaño.
Restamos el valor mínimo del valor máximo.

Ejemplo

Para una muestra (1, 45, 50, 55, 100), el dato menor es 1 y el dato mayor es 100. Sus valores se encuentran en un rango de:

Rango = 100 – 1 =99

Varianza

La varianza es una variable estadística que mide la dispersión de los valores respecto a un valor central (media), es decir, la media de las diferencias cuadráticas del las puntuaciones respecto a su media aritmética.

$S_X^2 = \frac{\sum_{i=1}^k (X_i - \bar{X})^2}{n}$

$S_X^2 = \frac{1}{n}\sum_{i=1}^k (X_i - \bar{X})^2 \cdot x_i$

Propiedades:

La varianza es siempre positiva o 0: $S_{X}^2 \geq 0$
Si a los datos de la distribución les sumamos una cantidad constante la varianza no se modifica.

$Y i = X i + k$

$S_Y^2 = \frac{\sum (Y_i - \bar{Y})^2}{n} = \frac{\sum [(X_i + k) - (\bar{X} + k)]^2}{n} = \frac{\sum (X_i + k - \bar{X} - k)^2}{n} = \frac{\sum (X_i - \bar{X})^2}{n} = S_X^2$

Si a los datos de la distribución les multiplicamos una constante, la varianza queda multiplicada por el cuadrado de esa constante.

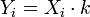
$Y_i = X_i \cdot k$

$S_Y^2 = \frac{\sum (Y_i - \bar{Y})^2}{n} = \frac{\sum (X_i \cdot k - \bar{X} \cdot k)^2}{n} = \frac{\sum [k \cdot (X_i - \bar{X})]^2}{n} = \frac{\sum [k^2 \cdot (X_i - \bar{X})^2]}{n} = k^2 \cdot \frac{\sum (X_i - \bar{X})^2}{n} = k^2 \cdot S_X^2$

Propiedad distributiva: $V (X + Y) = V (X) + V (Y)$

Desviacion Estandar

La varianza a veces no se interpreta claramente, ya que se mide en unidades cuadráticas. Para evitar ese problema se define otra medida de dispersión, que es la desviación estandar, que se halla como la raíz cuadrada positiva de la varianza. La desviación típica nos informa sobre la dispersión de los datos respecto al valor de la media; cuanto mayor sea su valor, más dispersos estarán los datos.

Desviación estadar muestral: 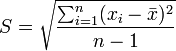$S = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}}$

Desviación estadar poblacional: $\sigma = \sqrt{\frac{\sum_{i=1}^n (X_i - \mu)^2}{N}}$

probabilidad y estadistica

sábado, 20 de septiembre de 2008

Datos no agrupados/Medidas de dispersion

Ejemplo

No hay comentarios:

Archivo del blog

Datos personales